SEMANA DEL 21 AL 24 DE JULIO
LECTURA Y ESCRITURA DE NÚMEROS DE CUATRO CIFRAS

4 unidades de mil = 40 centenas = 400 decenas = 4 000 unidades
6 decenas = 60 unidades
8 unidades.
Luego:
4 568 = 4 000 + 500 + 60 + 8
Ejemplo 2:
El número 7 509 está compuesto por
7 unidades de mil = 7 000 unidades
5 centenas = 500 unidades
0 decenas
9 unidades.
Luego:
7 509 = 7 000 + 500 + 9.
Y se lee:
Siete mil quinientos nueve.
MATH
SEMANA DEL 13 AL 17 DE JULIO
UNIDADES DE MIL

MATH
SEMANA DEL 1 AL 5 DE JUNIO
MULTIPLICACIONES POR UNA CIFRA
math
semana del 25 al 29 de mayo
los términos de la multiplicación


Math
semana del 19 al 22 de mayo
Esta semana trabajaremos las tablas salteadas deben repasar se realizara una prueba

MATH
Semana del 11 al 15 de mayo
problemas matematicos

MATH
SEMANA DEL 4 al 8 de mayo
TABLAS DE MULTIPLICAR DEL 8 y el 9
tablas del 8 y el 9



semana del 17 al 30 de abril


semana del 7 al 10 de abril
LA MULTIPLICACIÓN

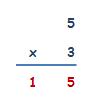

revisar edutracer estan las tareas asignadas
semana del 16 al 20
Unión e intersección de un conjunto
En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto, cuyos elementos son los elementos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos p el
conjunto de los números impares positivos I
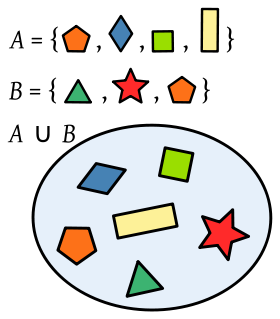
En teoría de conjuntos, la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de los números pares P y el conjunto de los cuadrados C de números naturales, su intersección es el conjunto de los cuadrados pares D :
HOMEWORK
Semana del 9 al 13 de febrero
CONJUNTOS

Amiguitos aquí les subí este vídeo sobre conjuntos
LECTURA Y ESCRITURA DE NÚMEROS DE CUATRO CIFRAS

4 unidades de mil = 40 centenas = 400 decenas = 4 000 unidades
| Y se lee: Cuatro mil quinientos sesenta y ocho. |
6 decenas = 60 unidades
8 unidades.
Luego:
4 568 = 4 000 + 500 + 60 + 8
Ejemplo 2:
El número 7 509 está compuesto por
7 unidades de mil = 7 000 unidades
5 centenas = 500 unidades
0 decenas
9 unidades.
Luego:
7 509 = 7 000 + 500 + 9.
Y se lee:
Siete mil quinientos nueve.
MATH
SEMANA DEL 13 AL 17 DE JULIO
UNIDADES DE MIL

MATH
SEMANA DEL 1 AL 5 DE JUNIO
MULTIPLICACIONES POR UNA CIFRA
math
semana del 25 al 29 de mayo
los términos de la multiplicación

Math
semana del 19 al 22 de mayo
Esta semana trabajaremos las tablas salteadas deben repasar se realizara una prueba

MATH
Semana del 11 al 15 de mayo
problemas matematicos

MATH
SEMANA DEL 4 al 8 de mayo
TABLAS DE MULTIPLICAR DEL 8 y el 9
Esta semana estudiamos y aprendimos las tablas de multiplicar por 8 y por 9.
tablas del 8 y el 9



semana del 17 al 30 de abril
Tabla del 2: multiplica de par en par.
Para calcular el resultado de la tabla del 2 puedes saltar al resultado del siguiente número par. De esta manera: 2×1=2, 2×2=4, 2×3=6 y así sucesivamente. Otro truco para aprender esta tabla es tener en cuenta que el resultado siempre es el doble del número por el que se está multiplicando.
Tabla del 5: suma de 5 en 5.
Igual que la tabla del 2, la del 5 es muy fácil de aprender. Si la dices de corrido saltarás de una cifra que acabe en 5 a la siguiente, que tendrá 0. Por ejemplo: 5, 10, 15, 20, 25…
Si te la preguntan de forma aleatoria tampoco es difícil de responder. Calcula la mitad del número que te pregunten y multiplícalo por 10 (se hace solo poniendo un 0). Por ejemplo: 5×6. La mitad de 6 es 3. Multiplica 3 por 10 (o pon un 0 al final). Te da 30.
Algo más difícil: 5 x 7. La mitad de 7 es 3,5. En este caso no pondrás 0 sino que al tener decimales, quitarás la coma al multiplicarlo por 10.
La Tabla del 9 tiene los trucos más originales.
Conocer los resultados de la tabla del 9 es mucho más sencillo de lo que parece. Solo tienes que imaginarte la tabla escrita delante y al lado haz dos filas. En la primera marca todos los números de una decena desde el final hasta el principio. Así: 9, 8, 7, 6, 5, 4, 3, 2, 1, 0.
A la izquierda de cada uno de ellos coloca los mismos números pero contando a la inversa. De esta manera: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ahora une esta fila con la anterior. Te quedará así: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90.
Estos números corresponden con los resultados de la multiplicación: 9×1=9, 9×2=18, 9×3=27, 9×4= 36 y así sucesivamente.
Otro truco para aprender la tabla del nueve es utilizar las manos. Estiras los dedos de las dos manos y pones tus manos frente a tu rostro con el dedo meñique de tu mano izquierda hacia la


semana del 7 al 10 de abril
LA MULTIPLICACIÓN

Multiplicar es lo mismo que sumar varias veces el mismo número:
Por ejemplo:
2 x 3 es lo mismo que sumar el número 2 tres veces (2 + 2+ 2)
6 x 5 es lo mismo que sumar el número 6 cinco veces (6 + 6 + 6 + 6 + 6)
Cuando vamos a hacer una multiplicación, por ejemplo 5 x 3, la escribimos de la siguiente manera:
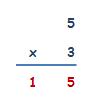
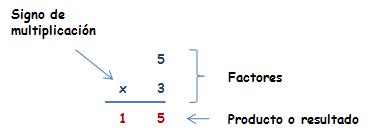
Los términos de la multiplicación son: Factores y Producto (o resultado).

revisar edutracer estan las tareas asignadas
semana del 16 al 20
Unión e intersección de un conjunto
En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto, cuyos elementos son los elementos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos p el
conjunto de los números impares positivos I

En teoría de conjuntos, la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de los números pares P y el conjunto de los cuadrados C de números naturales, su intersección es el conjunto de los cuadrados pares D :
HOMEWORK
Semana del 9 al 13 de febrero
CONJUNTOS
La palabra conjunto generalmente la asociamos con la idea de agrupar objetos, por ejemplo un conjunto de discos, de libros, de plantas de cultivo y en otras ocasiones en palabras como hato, rebaño, piara, parcelas, campesino, familia, etc., es decir la palabra conjunto denota una colección de elementos claramente entre sí, que guardan alguna característica en común. Ya sean números, personas, figuras, ideas y conceptos.







